如何为精密设备“隔离”振动？——深入解析被动隔振原理与关

如何为精密设备“隔离"振动？——深入解析被动隔振原理与关键参数

在前期内容中，我们已认识到振动对精密设备的 “隐形伤害"，并掌握通过 VC 曲线开展 “环境体检" 的方法。当振动问题浮现，被动隔振作为应用zui广泛的解决方案，凭借无需外部能量、成本低、可靠性高的优势，成为多数精密设备的shou选。本文将聚焦被动隔振，系统拆解其物理本质、核心原理、设计逻辑与性能评估标准，为被动隔振方案的选型与设计提供理论支撑。

一、       隔振的本质：打造一个安静的“微环境"

隔振的核心目标并非消除所有振动 —— 现实中无法实现，而是在振动源头（如地面、设备周边环境）与受保护的精密设备之间，构建一个 “振动过滤器"。该过滤器通过改变振动能量的传递路径与效率，大幅衰减传递至设备的振动能量，将振动影响控制在设备允许的精度范围内，最终保障设备运行精度、数据可靠性与使用寿命，为设备创造相对静止的 “微环境"。

以半导体行业 7 纳米芯片光刻工艺为例，光刻机工作台需在纳米级精度下完成移动。若地面传递 0.01 毫米（约头发丝直径 1/5）的振动，会直接导致光刻图案偏移，造成晶圆报废。此时，被动隔振技术需将外界振动对工作台的影响控制在 “亚纳米级"，通过弹性与阻尼元件的协同作用，为光刻过程构建 “振动可忽略" 的稳定环境，这正是被动隔振本质的典型体现。

二、被动隔振核心概念与关键性能参数

理解被动隔振的基础是掌握其核心概念与性能指标，这是后续原理分析与设计的前提。

1、基础概念定义与作用

2.       关键性能参数解析

l                      隔振效率（η）：与振动传递率互补，计算公式为 η=(1-T)×100%。例如，当 T=0.2 时，η=80%，表示 80% 的振动能量被隔离，仅 20% 传递至设备，直观反映被动隔振系统的能量衰减能力。

l                      共振峰值（Tmax）：被动隔振系统在共振点（r=1，即激励频率 = 固有频率）时的最大传递率。忽略阻尼时，Tmax趋近于无穷大；实际应用中，需通过合理设计阻尼，将 Tmax控制在＜5 的安全范围，避免共振导致设备结构损坏或精度失效。

l                      频率响应范围：被动隔振系统有效工作的频率区间， f> f0的频段。例如，若系统

f₀=2Hz，有效隔振范围为 f＞2.828Hz，无法对 2.828Hz 以下的低频振动起到隔离作用，这是被动隔振的固有特性。

三、被动隔振（Passive Vibration Isolation）核心原理：单自由度质量 - 弹簧 - 阻尼系统

被动隔振是zui常用的隔振方式，无需外部能量输入，仅通过弹性元件（如弹簧、橡胶）、阻尼元件（如阻尼器）构成的系统改变振动传递特性。

最基础且最重要的理论模型是单自由度质量-弹簧-阻尼系统（图1）。它抽象地描述了被动隔振系统的核心物理特性，是所有复杂隔振器设计的理论基石。

1、系统模型构成

该系统是理解被动隔振的基础模型，包含三个基本元素：

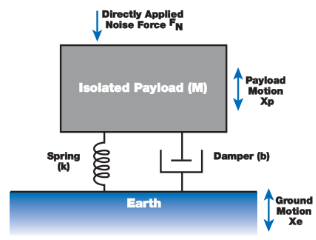
           图1

l                      被隔离的质量块（M：被隔振负载的质量）： 代表需要被隔离的负载，在此处被简化为一个无内部共振的单质量块（单位：kg）。

l                      弹簧（k：弹簧的刚度）： 代表隔振器的弹性支撑元件（如TMC气动隔振器中的空气弹簧），作用是支撑负载，并对负载施加一个力，该力由以下公式给出：

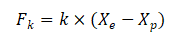
其中和和分别代表地面（振源）和负载的动态位置；弹簧刚度 k 越小，系统固有频率 f₀越低，越容易进入有效隔振区。

l                      阻尼器（b：阻尼系数）：代表消耗振动能量的元件如TMC Gimbal Piston中的阻尼孔、MaxDamp中的阻尼油），通过将质量块的动能转化为热量（如阻尼孔中流体的摩擦热）实现能量耗散，最终使系统恢复静止。这是通过产生一个与负载相对于地面的速度成正比且方向相反的力来实现的：

从力学公式可见，两个方程中都存在，地面振动通过弹簧与阻尼器以力的形式传递至被隔离质量块，被动隔振的核心就是通过调整 k、b、M 的参数，改变振动传递效率，实现 “过滤" 振动的目标。

2、       振动传递率公式与曲线特征

通常，我们不使用参数M，k，b和来描述系统，而是定义一组新的参数，这些参数能更直接地与质量-弹簧系统的可观测特性相关联。

第一个是固有频率：

它描述了在没有任何阻尼（b=0）的情况下，系统自由振荡的频率。通常使用以下两个常见参数之一来描述系统中的阻尼：品质因子Q和阻尼比ζ

这个理想化系统的传递率为：

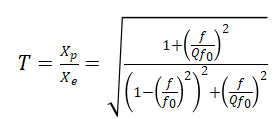         （1）

下图绘制了对于几个不同的品质因子Q，系统传递率随频率比变化的曲线。所绘制的Q值范围从0.5到100。Q=0.5的情况是一个特例，称为临界阻尼，是指当系统发生位移后释放时，不会超过平衡位置的阻尼水平。阻尼比就是系统阻尼与临界阻尼的比值。我们使用Q而不是ζ，是因为因为对于Q 大于约2的情况下，在ω=ω0的时候，T≈Q。（其中ω和ω0为角频率，ω=2πf）。

图2

不同 Q 值（阻尼水平）的系统，传递率随频率比 r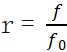（，f为激励频率，f0为固有频率） 的变化呈现明确规律，可分为三个阶段

l                      同步振动段（r＜1，即 f＜f₀）：T≈1，被隔离质量块随地面同步运动，弹簧与阻尼器无法起到隔振作用。例如，当地面振动频率为 1Hz，系统 f₀=2Hz 时，设备会跟随地面 1Hz 的振动同步晃动，无隔振效果。

l                      共振危险段（r≈1，即 f≈f₀）：T＞1，振动被放大，放大倍数约等于 Q 值（Q 越大，共振峰值越高）。若此时 Tmax＞5，可能导致设备结构变形或精度失效，需通过增大阻尼（减小 Q）降低共振峰值。

l                      有效隔振段（r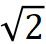＞，即 f＞ f₀）：这是隔振器发挥作用的区域。T 随 r² 的增大而减小，隔振效果逐渐增强。此时阻尼越小（Q 越大），T 值越小，隔振效果越好。可见低阻尼在有效隔振段更具优势。

这一曲线清晰揭示了被动隔振的核心矛盾：阻尼增大可抑制共振，但会削弱有效隔振效果；阻尼减小能提升有效隔振效果，但会加剧共振风险，设计时需根据实际场景平衡二者关系。

直接施加在负载上的力传递到负载的运动幅值，其形式与公式1表达的略有不同。这个传递函数具有单位力引起的位移的量纲（如 m/N），因此不应与（无量纲的）传递率混淆：

下图绘制了此函数随频率变化的曲线，降低 Q 值会在所有频率减小负载的响应。

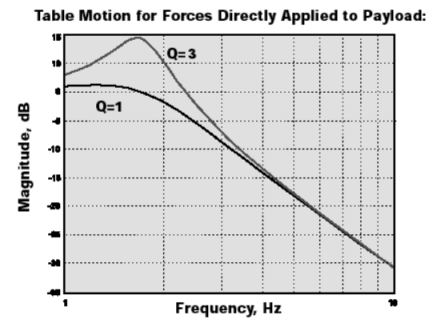
图3

TMC的MaxDamp®隔振器正是利用了这一特性，适用于主要扰动产生于被隔振负载本身的应用。图4显示了与图3中曲线相对应的负载的时域响应。该图也说明了系统一旦受到扰动后的衰减情况。衰减的包络线为 。

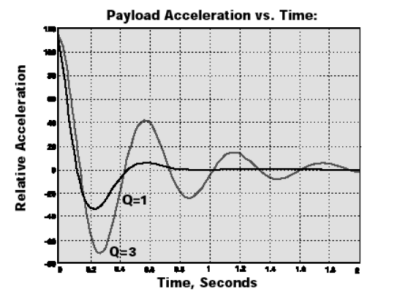
图4

实际系统与图1所示的简单模型存在一些显著差异，最重要的一点是实际系统具有六个运动自由度((DOF)。这些自由度并非独立，在大多数系统中存在强烈的耦合。例如，“水平传递函数"通常显示两个共振峰，因为负载的水平运动会引起倾斜运动，反之亦然。

四、       隔振器的设计目标、思路与关键权衡

（一）核心设计目标

被动隔振器的设计核心是 “匹配固有频率 f₀与阻尼比 ζ"，实现两大目标：

(1)                      确保系统能进入有效隔振区（r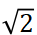＞），即让设备实际面临的主要振动频率 f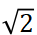＞f0

(2)                      将共振峰值控制在安全范围，避免共振对设备造成损害。

因此，隔振器最核心的设计目标非常明确。根据固有频率公式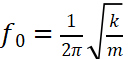，降低 f₀是扩大有效隔振区的关键 ——f₀越低，有效隔振区的起始频率（ f0）越低，能覆盖更多低频振动场景（如地面常见的 2-10Hz 振动）。其中：k是隔振器的刚度（越“软"越好）m是隔振器所承载的质量（越“重"越好）。

（二）具体设计思路

设计思路因此清晰，降低 f₀主要有两大途径：

1.                      降低弹性元件刚度 k选用 “更软" 的弹性元件，减少单位位移所需的力，从而降低系统刚度。例如：

TMC 气浮隔振器利用压缩空气的低刚度特性，垂直刚度可低至 10N/m 以下，使系统 f₀降至 1.5-2.0Hz；

橡胶隔振器通过选用低硬度橡胶材料（如邵氏硬度 30-50 度），降低刚度，适用于中低频振动隔离。

2.                      增加被隔离质量 M，在弹性元件刚度固定时，增大被隔离质量可直接降低 f₀。

例如：

精密光学设备常用 500-1000kg 的花岗岩平台作为底座，通过增大 M，配合空气弹簧的低 k 值，使系统 f₀降至 2Hz 以下；

半导体检测设备通过加装铸铁配重块（质量可达 200kg 以上），提升系统稳定性的同时，降低 f₀。关键权衡：“隔振性能" vs “系统稳定性"

（三）       关键设计权衡

被动隔振设计中存在两大核心权衡，需根据设备场景灵活调整：

1、       “低 f₀" 与 “静态稳定性" 的权衡

系统越 “软"（k 越小，f₀越低），隔振效果越好，但受扰动后（如人员走动、设备内部运动）的恢复时间越长，静态稳定性越差。例如，f₀=1Hz 的系统受扰动后，恢复至静止状态需 5-10 秒；而 f₀=5Hz 的系统恢复时间仅需 0.5-1 秒。

优化方案：控制静态沉降量 ，同时通过优化设备重心（如降低重心高度），提升抗倾覆能力。

2、       “共振抑制" 与 “有效隔振" 的权衡

增大阻尼（ζ 增大）可降低共振峰值，但会导致有效隔振区的 T 值增大，隔振效率下降；减小阻尼（ζ 减小）能提升有效隔振效率，但会使共振峰值升高。

优化方案：根据激励频率与 f₀的比值 r 调整 ζ：

若 r＞3（激励频率远离 f₀，共振风险低）：取小阻尼（ζ=0.05-0.1），优先保证有效隔振效果；

若 r=1.5-2（激励频率接近 f₀，共振风险高）：取大阻尼（ζ=0.2-0.3），优先抑制共振峰值。

五、 被动隔振设计常见误区与优化方向

在被动隔振方案设计与选型中，易因对原理理解不深入导致效果不佳，以下是三大常见误区及优化建议：

误区 1：盲目追求低固有频率 f₀

问题：过度降低 f₀会导致静态沉降量 δst 大幅增大，可能引发高重心设备（如立式光刻机）倾覆，或使弹性元件（如弹簧）因过度压缩而永jiu损坏；同时，过低的 f₀会延长系统扰动恢复时间，影响设备动态稳定性。

优化方向：根据设备使用场景设定合理 f₀：

低频振动环境（如实验室地面 2-5Hz 振动）：f₀控制在 1.5-2.5Hz，确保f₀＜2Hz，覆盖低频振动；

中高频振动环境（如工厂车间 10-50Hz 振动）：f₀控制在 3-5Hz，平衡稳定性与隔振效果；严格控制静态沉降量，避免调平困难。

误区 2：忽视阻尼的双重作用，过度增减阻尼

问题：部分设计中为追求 “ji致隔振"，过度减小阻尼（ζ＜0.05），导致共振峰值 Tmax＞5，设备在共振频率下运行时精度严重受损；或为 “避免共振"，过度增大阻尼（ζ＞0.3），使有效隔振区 T 值＞0.3（隔振效率＜70%），无法满足精密设备需求。

优化方向：基于激励频率分布调整阻尼：

先通过 VC 曲线检测环境振动频率，确定主要振动频率 f 与系统 f₀的比值 r；

若 r＞3，选 ζ=0.05-0.1（如气浮隔振器搭配低阻尼阻尼器）；

误区 3：弹性元件与负载不匹配，刚度或承载能力失衡

问题：弹性元件选型时，未根据 “设备重量 + 底座重量" 精确匹配刚度与承载能力：

刚度过高（k 过大）：导致 f₀过高，有效隔振区起始频率f₀＞主要振动频率，无隔振效果；

承载能力不足（弹性元件额定负载＜实际负载）：弹性元件yong久变形，刚度失效；

承载能力过剩（额定负载远大于实际负载）：弹性元件形变量过小，无法起到 “软支撑" 作用，f₀偏高。

优化方向：精确计算总负载 Mtotal = 设备重量 + 底座重量，根据 f₀目标值，通过公式计算所需刚度；选择弹性元件时，确保其额定负载为 Mtotal 的 1.2-1.5 倍，避免超载或负载不足；

多支点隔振（如 4 个隔振器支撑设备）时，需保证各支点负载均匀，避免弹性元件受力不均导致刚度偏差。

六、 总结与TMC的实践

隔振并非 “越严格越好"，而是需要基于 VC 曲线评估结果，结合实验精度需求、环境振动特性，选择方案。TMC 的隔振技术之所以能在全球精密领域广泛应用，核心在于其始终以 “理论为基、场景为导向"—— 从经典的Gimbal Piston™气浮隔振器到高阻尼的MaxDamp®系列，其设计都严格遵循这些基础原理，并在工程上做到了ji致，为客户在不同应用场景下提供隔振解决方案。

下一篇内容，我们将进一步聚焦 TMC 被动隔振产品的具体结构设计、参数选型方法及典型行业应用案例，帮助大家更好地掌握被动隔振方案的选型与应用，敬请期待！

---